Let's know about the types of ratios?

Let's know about the types of ratios?

Ratios are divided into two categories.

1. Direct proportion

2. Inverse proportion

What is the direct proportion? What is the inverse proportion? Today we will see that mathematically. Tomorrow we will see how it relates to life.

You will learn about equivalent fractions when you read about fractions. Never mind if you don't know about it or don't remember about it.

Now let's look at equivalent fractions.

When you asked for an example of a fraction yesterday, you said ¼, didn't you?

Let's take that.

Multiplying this ¼ up and down by two gives what?

Are you saying it will be 2/8?

That is equivalent fraction.

Multiplying this ¼ up and down by three, what does it get?

You mean 3/12?

This is also its equivalent fraction.

So if you multiply ¼ up and down by four, by five, by six, … and so on and so on, are they also equal fractions?

Do you understand now?

Want a little more insight?

Well let's see that too.

What is ¼?

¼ refers to one part of a substance when it is divided into four parts.

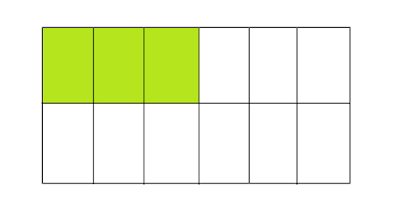
That is, let us take a rectangular shape as shown in the figure. You can think of this rectangular shape as a loaf of bread. Or consider it your favorite snack. If we divide it into four parts and mark one part of it, it is ¼, isn't it? Shall we paint green only for that one part?

Now see what we have done in the picture.

Now try making the four parts into eight parts. How do you say that? See the picture. Has it become eight? Now look at the part we colored green. Split into two parts? Does it become a fraction of 2/8?

That is, the size has not changed. Parting is changing. That means the number of parts is variable. The amount of green color we take in hasn't changed either. But the number of parts has increased. That's it.

If we divide 4 parts into 8 parts in the picture then the part size we take i.e. green color becomes 2 parts. This is what we have done when we multiply ¼ up and down by two. That means both are the same size. But the change is only in the number of parts. That is, both fractions represent the same quantity, but there is a change in the number of different parts. This is what we call equivalent fractions.

Similarly, if ¼ is multiplied up or down by three, the result is the same. Check out the picture below. Multiplying ¼ up and down by three is 3/12? Then 12 parts should be put. Our green color should become three parts. See how it has changed.

So this is equivalent fraction. Same size i.e., The quantity is the same, although the number of parts vary, just as we are apt to divide.

To put it a little more clearly, a loaf of bread is still a loaf even if it is broken in two. Even if it is broken into four, it is still one loaf. Why is it the same bread even if it is broken into eight or sixteen? We can refer to those broken loaves as equal loaf of one loaf. So is an equivalent fraction.

Do you understand it now?

These equivalent fractions are proportional.

So what is inverse proportion? It's in the name itself.

A direct proportion is what we take in fractional form i.e. numerator and denominator form.

Then the inverse proportion is taken in multiplicative form i.e. in factored form.

If taken in fractional form it should be expressed as direct proportion and if taken in multiplicative form as inverse proportion.

That means if a / b is taken it is direct proportion.

If we take the same as a × b it is inverse proportion.

If we take ¼ in the last example we saw, it is a direct proportion. 1 × 4 is the inverse proportion.

If that is all, I have said this for your understanding.

Both direct proportion and inverse proportion contain a mathematical property. Want to know that. Will we find out tomorrow?